Generally neighborhood operations is performed by the following command
Syntax
B = nlfilter(A, [m n], fun)B = nlfilter(A, 'indexed',...)
Description
B = nlfilter(A, [m n], fun) applies the function fun to each m-by-n sliding block of the grayscale image A. fun is a function that accepts an m-by-n matrix as input and returns a scalar result.c = fun(x)
fun must be a function handle.
c is the output value for the center pixel in the m-by-n block x. nlfilter calls fun for each pixel in A. nlfilter zero-pads the m-by-n block at the edges, if necessary.
Example:-
lets us consider an image matrix D=[ 1 2 3;3 4 5;5 6 7]
D=

now we going to perform the energy operation on A . energy operation is defined as
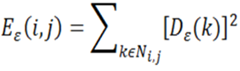
Where E represent the energy matrix , D is the input matrix and N represent the window of size m x n.
E = nlfilter(D, [3 3],@fun)
function c is given by
function c=fun(D)
y=0;
for i=1:numel(D)
y=x(i).^2+y;
end
c=y;
numel compute the no of element in matrix D i.e in this case it is 9
working of above script is given below
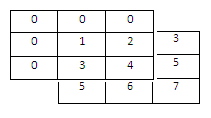
foe i=1
energy of 1 is obtained by addition of square of each value i.e ( 0^2 +0^2+0^2+0^2+1^2+2^2+0^2+3^2+4^2=30 )
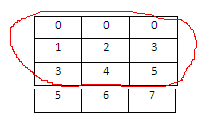
for i=2
energy of 2 is obtained by addition of square of each value i.e ( 0^2 +0^2+0^2+1^2+2^2+0^2+3^2+3^2+4^2+5^2=64 )
this procedure is repeated till i=9 and final energy matrix is given by
E=




No comments:
Post a Comment